【本站讯】近日，我校理学院李明教授团队在设备无关量子随机数研究方面取得重要进展，相关成果《基于链式不等式最大量子违背值紧的上界的设备无关随机性》(Device-independent randomness based on a tight upper bound of the maximal quantum value of chained inequality）发表于量子信息领域权威期刊Physical Review A。论文第一作者为硕士研究生肖友旺，通讯作者为李明。该研究工作得到山东省自然科学基金量子科学重点专项、学校自主创新基金强基计划资助。

量子非局域性是量子物理区别于经典物理最重要的性质之一，是实现量子密钥分发、量子随机数、量子计算和量子精密测量等现代量子信息处理任务的基础。关于量子非局域性和定域实在性的讨论可以追溯到上世纪六十年代，英国物理学家Bell在对两体纠缠态的研究中发现，基于非局域性与定域实在性的两体关联函数具有明显的可区分性，这就是著名的Bell不等式。2022年，诺贝尔奖委员会宣布诺贝尔物理学奖授予阿兰·阿斯佩克特(Alain Aspect)、约翰·克劳瑟(John F. Clauser)和安东·泽林格(Anton Zeilinger)，以表彰他们“进行了纠缠光子的实验，确立了对贝尔不等式的不成立，并开创了量子信息科学”。随机数在密码学、科学仿真、基础物理研究等方面具有重要应用。与无法提供安全随机性的经典随机数生成器不同，设备无关量子随机数生成器从量子力学固有的不确定性中产生随机数，量子随机数安全性仅仅与系统的输入、输出相关，而并不依赖于物理设备的质量和可信度，即使在极端条件下，设备本身不可信或受到第三方控制，该方案产生的随机比特仍然具有目前最高等级的安全性。因此，设备无关量子随机数发生器的设计是一个重要的物理问题。

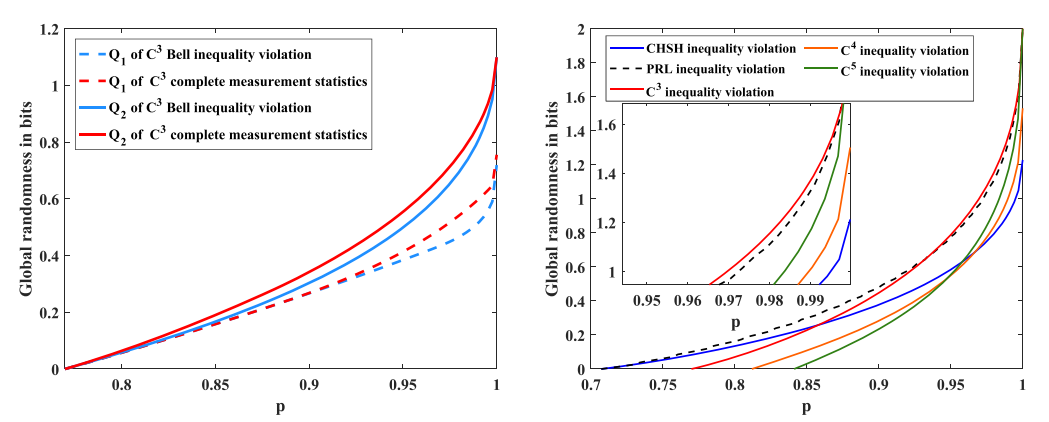
该论文推导了具有任意测量个数的链式不等式的紧的最大量子值的上界，并且得到了上界紧致的充分必要条件。基于此上界，利用含噪声的Werner态，通过不等式违反与全概率方法给出了在不同测量下的设备无关随机性的数量分析，结果表明该方案与其他方案（Phys. Rev. Lett. 129, 150403 (2022)）相比，在低噪声情况下选择三个测量个数的链式不等式所产生的设备无关随机性的量更高，这一工作揭示了多个测量的贝尔不等式在产生设备无关随机数中的意义，为发展新型量子信息处理任务奠定了重要基础。

李明教授团队长期致力于数学物理中量子信息与量子计算等方面的研究工作，先后主持国家自然科学基金、山东省自然科学基金量子科学重点专项等项目10余项，在Physical Review Letters、Physical Review A等著名期刊发表高水平论文70余篇， 在量子信息科学领域形成了一定的影响力。

论文链接：https://doi.org/10.1103/PhysRevA.107.052415